
In the last article we saw how we can derive the Normal Equation. So in this article we are going to solve the Simple Linear Regression problem using Normal Equation.
Normal Equation uses matrices to find out the slope and intercept of the best fit line. If you have read my previous articles then you might know that we have already implemented Simple Linear Regression using sklearn library in python and by building a function from scratch. So in this article we are going to find the equation of best fit line using Normal Equation that we derived in previous article.
Are you excited?
First we are going to start with a basic example with dummy data points and then we’ll see take the exact same dataset that we used in previous articles to find the value of co2 emission of a car. If you want to read my previous articles then here is the link for that.
Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
Simple Linear Regression From Scratch :
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-2fa88cd03e67
Introduction to Matrices For Machine Learning :
https://medium.com/@shuklapratik22/introduction-to-matrices-for-machine-learning-8aa0ce456975
If you want to watch the completely explained videos on Machine Learning algorithms and it’s derivation then here are the links for that:
(1) Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch :
https://youtu.be/bM3KmaghclY
(3) Simple Linear Regression Using Sklearn :
https://youtu.be/_VGjHF1X9oU
(4) Machine Learning Mathematic (Matrices) Explained :
https://youtu.be/1MASyeyAydw
Okay, so let’s get started.
Normal Equation is as follows :
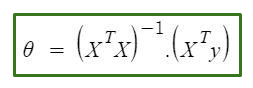
In the above equation :
θ : hypothesis parameters that define it the best.
X : input feature value of each instance
Y :Output value of each instance
We can even write this equation as :
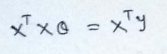
(1) Data points for which we want to find the line of best fit :
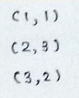
(2) The equation of best fit line is :
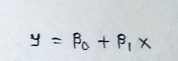
(3) Now we can write it in matrix form :
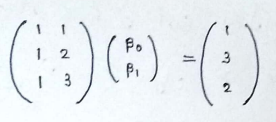
Here the first column will always be 1, because that is the coefficient of beta-0.The second column here will be the value of x-coordinate of the datapoint. On the other side of the equation we have the y-coordinate of our data points.
(3) So our X matrix will be :
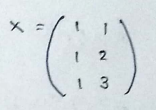
(4)Taking the transpose of matrix X :
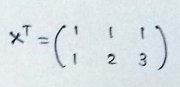
(5) Putting all the value in the equation :
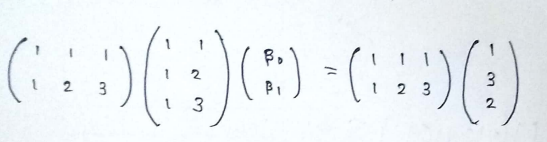
(6) After multiplication we get :
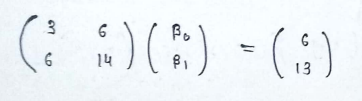
(7) Forming equations :
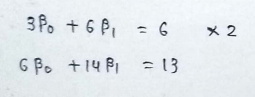
(8) Solving equations :
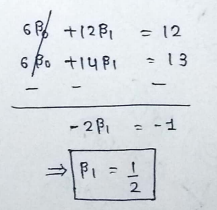
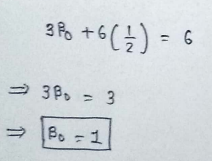
(9) Write the equation of best fit line :
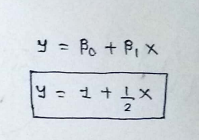
So here we found the equation of best fit line.Now we can predict any value of Y based on it’s x value.
Implementation In Python :
(1) Import the required libraries :
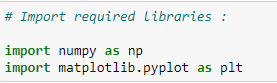
(2) Dataset :
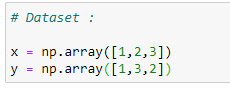
(3) Plot the data points :
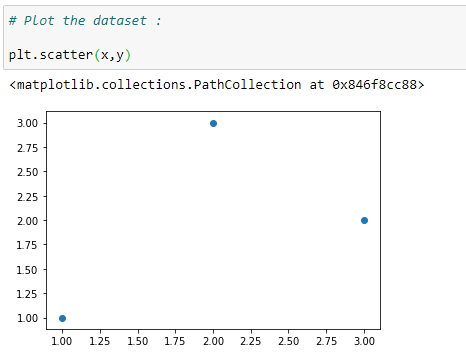
(4) Value of column-1 in our matrix X:

(5) Shape of X:
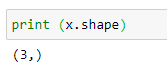
(6) Shape of X_bias :
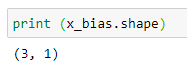
(7) We must change the shape of X to (3,1) to append them and form a matrix :
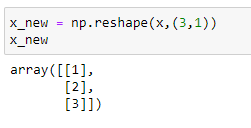
(8) Get the final Matrix X :
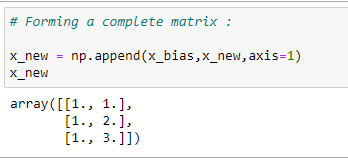
(9) Transpose of matrix X :
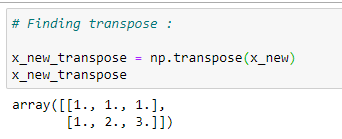
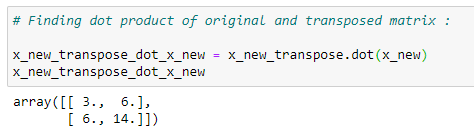
(10) Multiplication of Matrices :
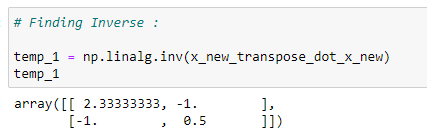
(11) Finding inverse :
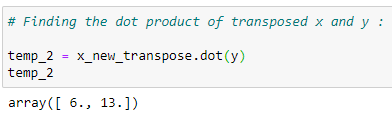
(12) Multiplication of Matrices :
(13)Finding slope and intercept :
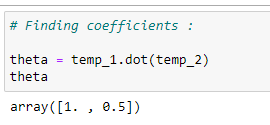
(14) Slope and Intercept:
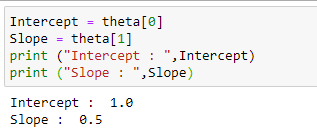
(15) Plot the best fit line :
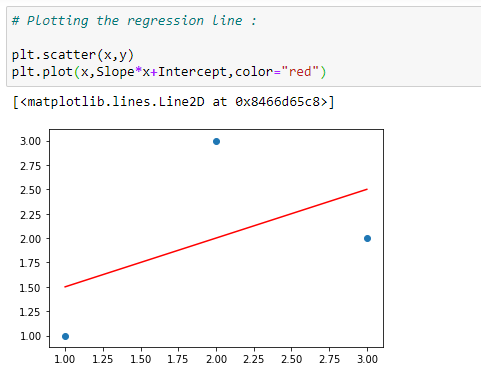
(16) Function to predict values :
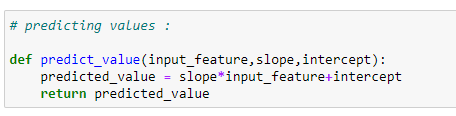
(17) Predicting values :
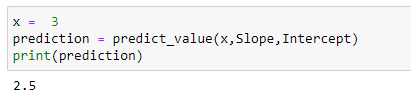
We can calculate the error and all but that logic remains the same as my previous article, so I’m not going to repeat it here again.
In case you want to have look at that:
Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
Finding Co2-Emission with Normal Equation :
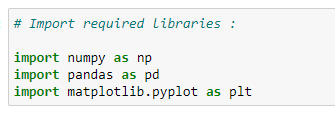
(1) Import the libraries :
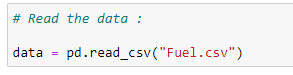
(2) Read the data set :
(3) Print the columns :

(4) Initialize our data :

(5) Type of data :
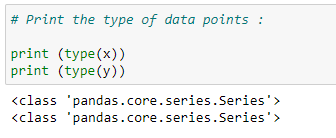
(6) We need array for our matrices :
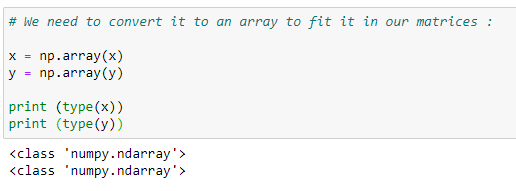
(7)Plot the data:
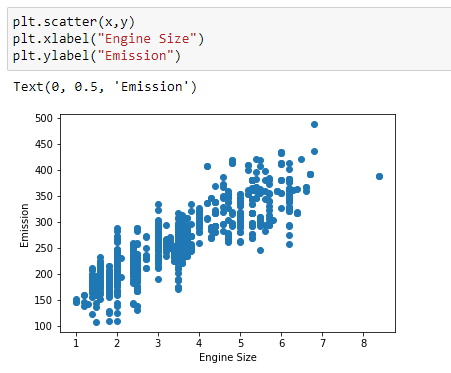
(8) Number of rows :
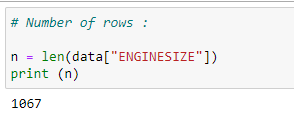
(9) Column-1 of matrix X:

(10) Reshaping the data :

(11) Forming matrix X :
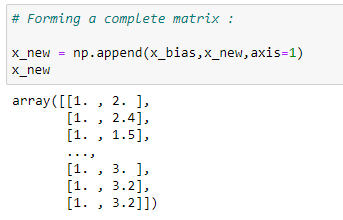
(12) Finding transpose:

(13) Matrix multiplication :
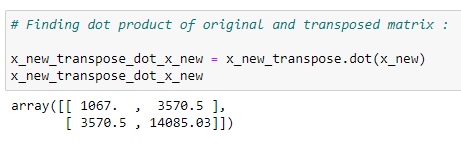
(14)Inverse of a matrix :
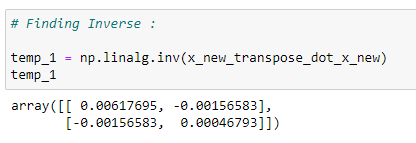
(15) Matrix multiplication :
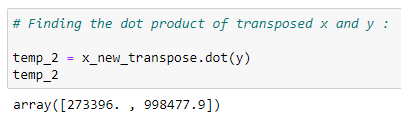
(16) Slope and intercept :
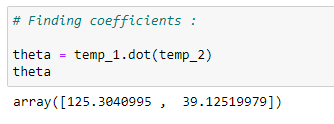
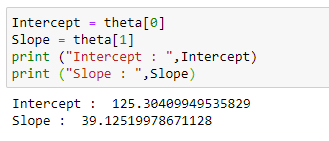
(17) Slope and Intercept :
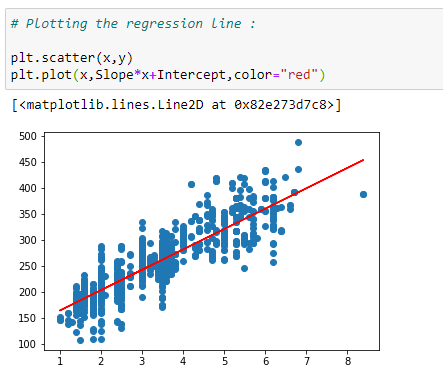
(!8) Plot the regression line :
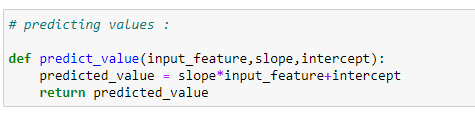
(19) Prediction function :
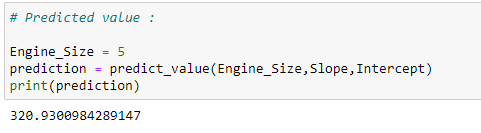
(20) predicted value :
We can find the accuracy of the model, but that is the same procedure as we did in my previous article.So here we are going to skip it.
So that was easier than what we did in our previous articles,right? See I told you!!
Moving Forward,
For more such detailed descriptions on machine learning algorithms and it’s derivation and implementation, you can follow me on my blog:
All my articles are available on my blog :
patrickstar0110.blogspot.com
Watch detailed videos with explanations and derivation on my youtube channel :
(1) Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch :
https://youtu.be/bM3KmaghclY
(3) Simple Linear Regression Using Sklearn :
https://youtu.be/_VGjHF1X9oU
(4) Machine Learning Mathematic (Matrices) Explained :
https://youtu.be/1MASyeyAydw
Read my other articles :
(1) Linear Regression From Scratch :
https://medium.com/@shuklapratik22/linear-regression-from-scratch-a3d21eff4e7c
(2) Linear Regression Through Brute Force :
https://medium.com/@shuklapratik22/linear-regression-line-through-brute-force-1bb6d8514712
(3) Linear Regression Complete Derivation:
https://medium.com/@shuklapratik22/linear-regression-complete-derivation-406f2859a09a
(4) Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
(5) Simple Linear Regression From Scratch :
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-2fa88cd03e67
(6) Gradient Descent With it’s Mathematics :
https://medium.com/@shuklapratik22/what-is-gradient-descent-7eb078fd4cdd
(7) Linear Regression With Gradient Descent From Scratch :
https://medium.com/@shuklapratik22/linear-regression-with-gradient-descent-from-scratch-d03dfa90d04c
(8) Error Calculation Techniques For Linear Regression :
https://medium.com/@shuklapratik22/error-calculation-techniques-for-linear-regression-ae436b682f90
(9) Introduction to Matrices For Machine Learning :
https://medium.com/@shuklapratik22/introduction-to-matrices-for-machine-learning-8aa0ce456975

wow great article
ReplyDelete