Introduction To Matrices (For Machine Learning)
In this article I’m going to show some basic operations that we can perform on matrices like addition, multiplication, adjoint and so on.
It’s very important for us to know how this operations work as we’re going to use matrices and it’s concepts a lot in machine learning algorithm.
These are just basic concepts that you might already have learn in high school. So let’s get started.

PART : 1
Definition of Matrix :
An m-by-n matrix is a rectangular array of numbers with m rows and n columns.
(1) 2*2 matrix with 2 rows and 2 columns :
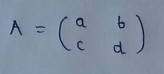
(2) 2*3 matrix with 2 rows and 3 columns :
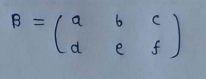
(3) 3*2 matrix with 3 rows and 2 columns :
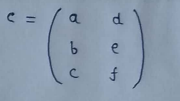
(4) Matrices with only 1 column are called column vectors:
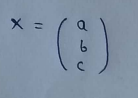
(5) Matrices with only 1 row are called raw vectors :
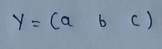
(6) Notation to write m*n matrix :

PART : 2
Addition and Multiplication of Matrix:
(1) Addition of matrices :
Matrices can be added only if they have the same dimensions.
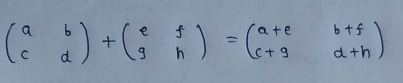
(2) Scalar multiplication :
It multiplies every number in matrix with a scalar value.
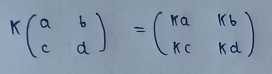
(3) Matrix Multiplication :
Matrices (other than the scaler) can be multiplied only if the number of columns of the left matrix is equals to the number of rows in the right matrix.
The multiplication of matrix is not commutative, it means A*B != B*A
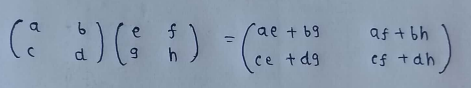
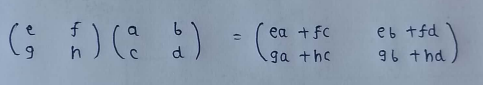
In general we can say that,
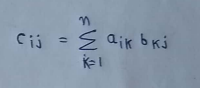
PART : 3
SPECIAL MATRICES :
(1) 0 matrix :
All elements of matrix are 0.
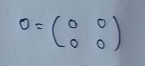
(2) Identity matrix :
The elements on the diagonal must be 1.
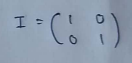
(3) Multiplying any matrix with identity matrix (I) doesn’t change the result.
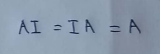
(4) Diagonal matrix :
A diagonal matrix has its only nonzero elements on the diagonal.
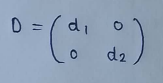
(5) Band Matrix :
All of the diagonal elements must be non-zero.
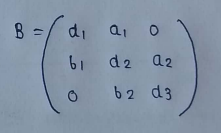
(6) Upper triangular matrix :
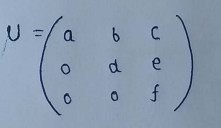
(7) Lower triangular matrix:
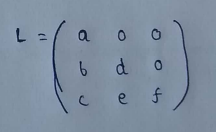
PART : 4
TRANSPOSE MATRIX
A transpose of a matrix, switches the rows and columns of A.


In other words we can say that,

(1) Example of transpose matrix :
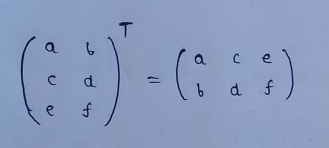
(2) Transpose of a transposed matrix :
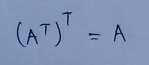
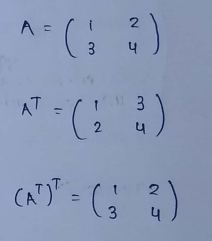
(3) Transpose of matrix addition :
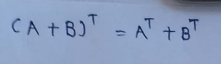
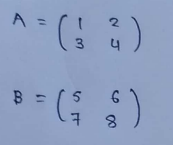
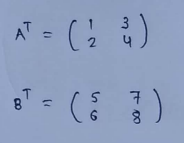
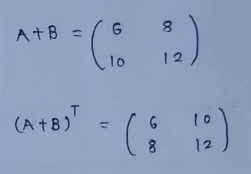
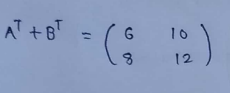
(3) Transpose of multiplied matrix :
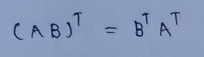
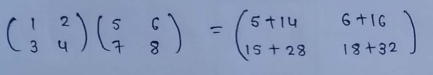

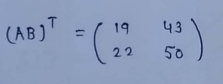
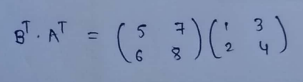
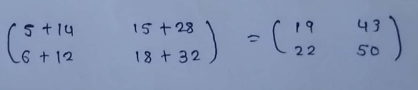
(4) Square matrix :
Number of rows must be equal to number of columns.
(a) Symmetric :
If the transpose of a matrix is equal to the original matrix then it’s called a symmetric matrix.
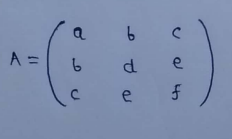
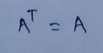
(b) Skew-symmetric :
If the transpose of the matrix equals to the negative of original matrix then it’s called Skew-symmetric matrix.
The diagonal elements must be 0 to form a skew symmetric matrix.
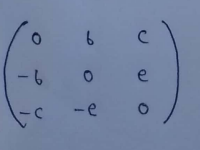
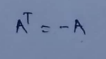
PART : 5
INNER AND OUTER PRODUCT :
Rules for multiplication of matrices :
(1) Number of columns of first matrix must be equal to number of rows of second matrix.
(2) Dimension of the multiplied matrix.
1st matrix : a*k
2nd matrix : k*b
Multiplied matrix will be of size : a*b
MULTIPLICATION:
(1) Inner product (or dot product or scalar product) between two vectors is obtained from the matrix product of a row vector times a column vector.A raw vector can be obtained from a column vector by a transpose operator.
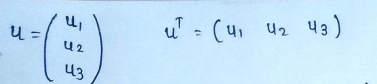
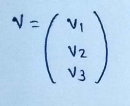

(2) If the inner product between two vectors is zero,we say that the vector is orthogonal.
The norm of the vector is defined by:
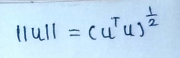
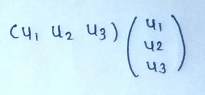
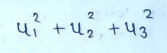
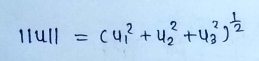
If the norm of a vector = 1 then we say that the vector is normalized. If the set of vectors are mutually orthogonal and normalized , we say that these vectors are orthonormal.
(3) An outer product of matrices is given as :
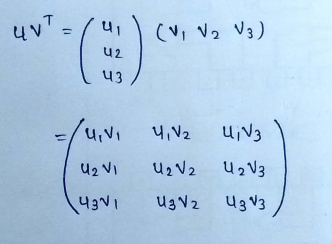
PART : 6
INVERSE OF MATRIX :
(1) 2*2 matrix :
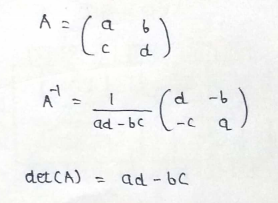
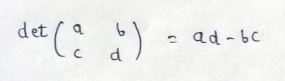
(2)3*3 matrix :
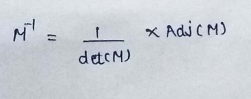
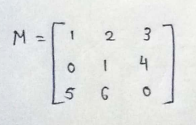
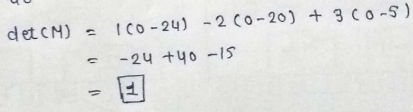
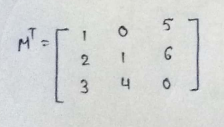
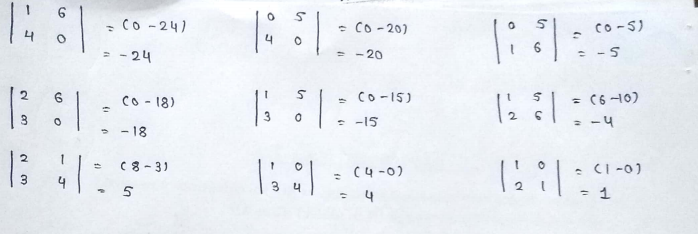
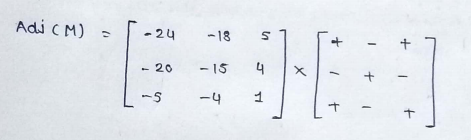
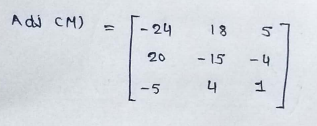
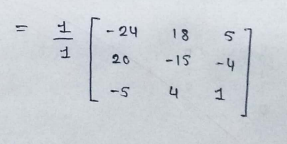
PART : 7
Gaussian Equation :
Consider the linear system of equations given by:
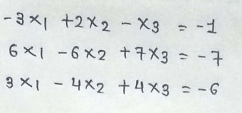
Which can be written in matrix form as :
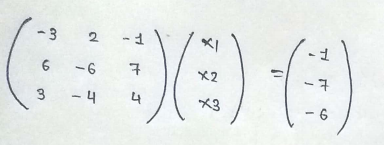
or symbolically Ax = b
The standard numerical algorithm used to solve a system of linear equations is called Gaussian Elimination. We first form what is called a augmented matrix by combining the matrix A with the column vector b.

Row reduction is the performed on this augmented matrix.
Rules:
(1) You can interchange the order of any row.
(2) You can multiply any row with constant.
(3) You can add a multiple of one row to another row.
These three operations do not change the solution of the original equations.
The goal here is to convert the matrix A into upper triangular form, then use this form to quickly solve for the unknowns x.
(1) First we multiply 1st row with 2 and add it to 2nd row.
(2) Then we add the 1st row to the 3rd row.
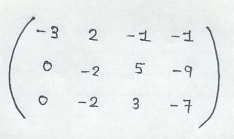
(3) Then we multiply the 2nd row with -1 and add it to 3rd row.

The original matrix has been converted to an upper triangular matrix. Now we can write the equations as follow.
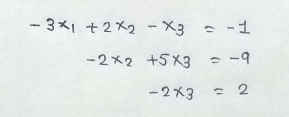
Solving these equations :
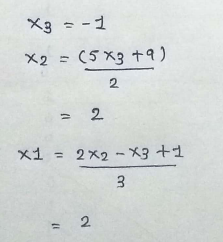
We have thus found the solution :
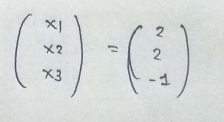
PART : 8
How to find sum of square of each elements in a matrix :
If we just multiply the matrix by itself then it don’t give us the square of it. So to do it we have to multiply it with its transpose. The result of that is, we get the sum of squared numbers of each row on the diagonal.
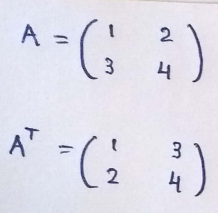
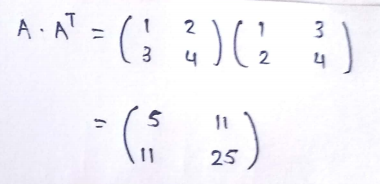
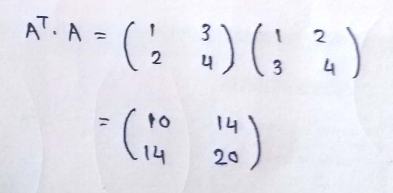
For vectors only we can easily find the sum of it’s element’s square easily. This is a very useful operation in matrix and we are going to use it in our next derivation!
Let’s find out how it works.
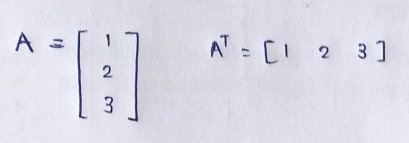
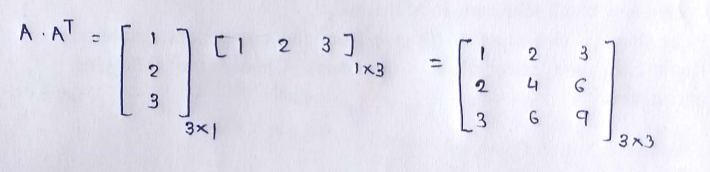
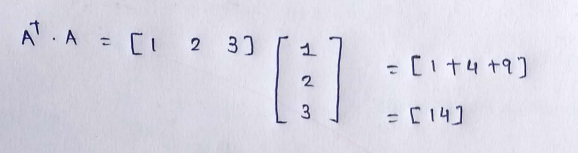
Here notice that 1²+2²+3³ = 14.
PART : 9
Given that A and B are vectors then we can say that,
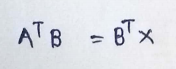
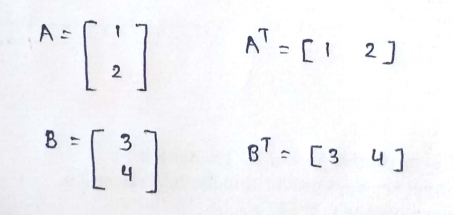
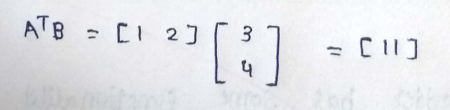
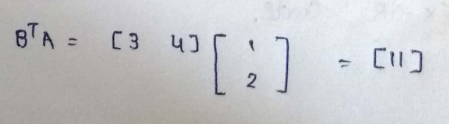
I hope you guys enjoyed it.
Moving Forward,
In the next article we will derive the Normal Equation for Linear Regression using the concepts we learned in this article.
For more such detailed descriptions on machine learning algorithms and it’s derivation and implementation, you can follow me on my blog:
All my articles are available on my blog :
patrickstar0110.blogspot.com
Watch detailed videos with explanations and derivation on my youtube channel :
(1) Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch :
https://youtu.be/bM3KmaghclY
(3) Simple Linear Regression Using Sklearn :
https://youtu.be/_VGjHF1X9oU
Read my other articles :
(1) Linear Regression From Scratch :
https://medium.com/@shuklapratik22/linear-regression-from-scratch-a3d21eff4e7c
(2) Linear Regression Through Brute Force :
https://medium.com/@shuklapratik22/linear-regression-line-through-brute-force-1bb6d8514712
(3) Linear Regression Complete Derivation:
https://medium.com/@shuklapratik22/linear-regression-complete-derivation-406f2859a09a
(4) Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
(5) Simple Linear Regression From Scratch :
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-2fa88cd03e67
(6) Gradient Descent With it’s Mathematics :
https://medium.com/@shuklapratik22/what-is-gradient-descent-7eb078fd4cdd
(7) Linear Regression With Gradient Descent From Scratch :
https://medium.com/@shuklapratik22/linear-regression-with-gradient-descent-from-scratch-d03dfa90d04c
(8) Error Calculation Techniques For Linear Regression :
https://medium.com/@shuklapratik22/error-calculation-techniques-for-linear-regression-ae436b682f90

This post is quite educative, I have been able pick a whole lot on matrices and other topics as a beginner. I hope to see more topics touched on this channel. Thank you
ReplyDelete