
In my previous articles I wrote about how we can plot regression line for our dataset . That was cool right! But there was also a problem that we were getting less accuracy for our model. Our ultimate goal is always to build a model with maximum accuracy and minimum errors. So In this article we’ll see how we can implement polynomial regression that best fits our data by using curves.
Before going there, here are some basic polynomial functions with its graphs plotted. This will help you understand better on which polynomial to use for a specific dataset.
Enjoy the article!
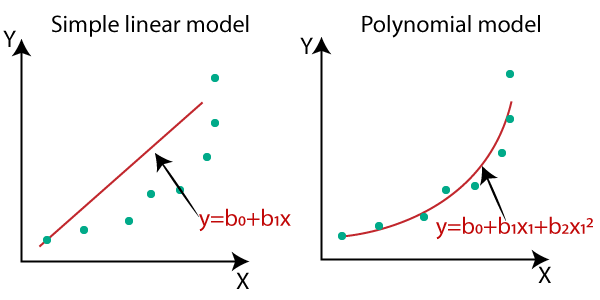
Polynomial Functions And Their Graphs :
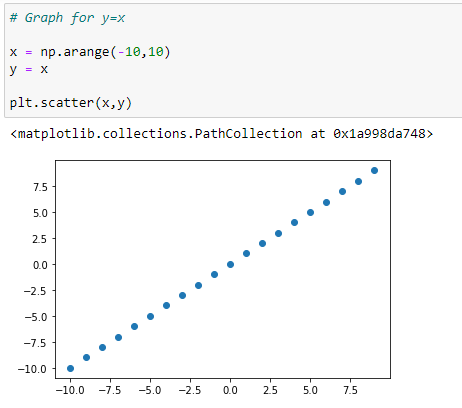
(1) Graph for Y=X :
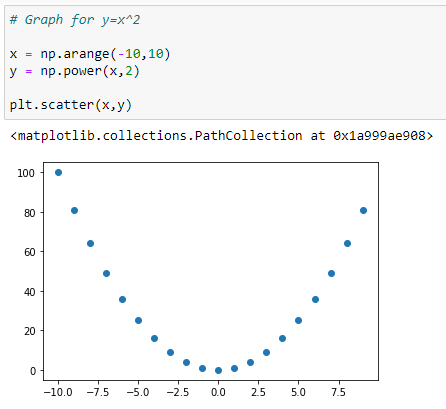
(2) Graph for Y = X² :
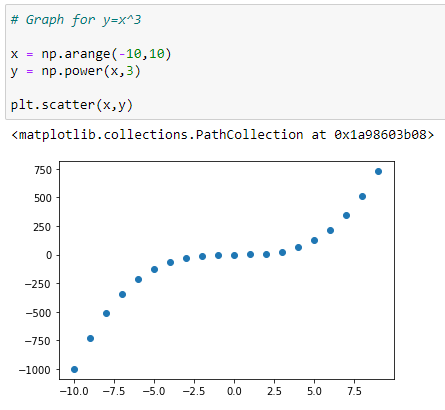
(3) Graph for Y = X³ :
(4) Graph with more than one polynomials : Y = X³+X²+X :
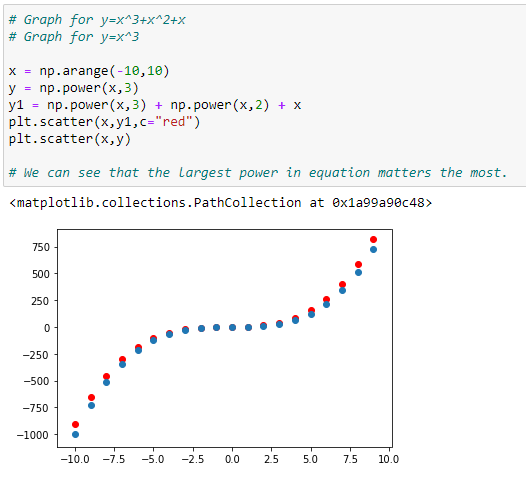
In this graph you can see that the red dots shows the graph for Y=X³+X²+X and the blue dots shows the graph for Y = X³. Here you can clearly see that the biggest power influence the shape of our graph.
Okay, so let’s get started on the cool parts! :)
Okay so now we are going to see why we should use polynomial (non linear) regression. Here I’m going to take an example and then for the First section I will find the linear regression line and calculate the error for that For Second section I will use polynomial regression and find the curve that best fits it and calculate the error. After then we will compare both of these error to see which model performed better.
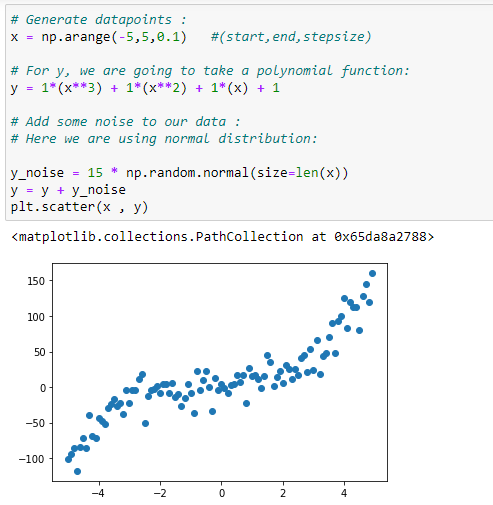
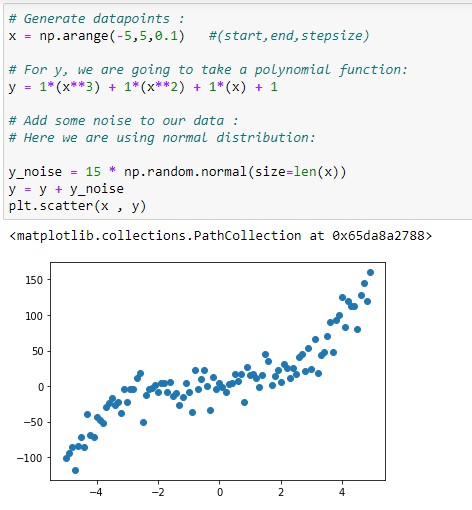
Here I’m taking this polynomial function for generating dataset, as this is an example where I’m going to show you when to use polynomial regression. I’m going to add some noise so that it looks more realistic!
Here we are going to implement linear regression and polynomial regression using Normal Equation. You can click here for such detailed explanatory videos on various machine learning algorithms.
Let’s move forward,
Normal equation is as follow :
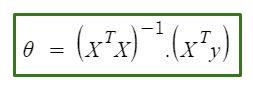
In the above equation :
θ : hypothesis parameters that define it the best.
X : input feature value of each instance
Y :Output value of each instance
Simple Linear regression :
Hypothesis Function For Simple Linear Regression :
y = beta_0 + beta_1 * x
Let’s code :
(1) Import required libraries :
(2) Dataset generation :
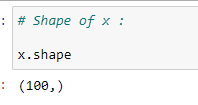
(3) Shape of x :
(4) Column-1 of our main matrix :
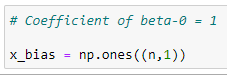
Here column-1 will always be the value off coefficient of beta_0 which will always be 1. But to create a matrix we need to consider it as a column. For better understanding click here

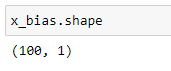
(5) Shape of x_bias :
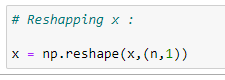
(6) As we need to append x with x_bias it must be of same shape:
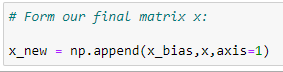
(7) Final matrix x :
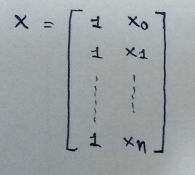
(8) Transpose of a matrix :
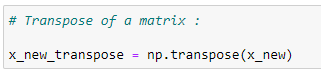
(9)Matrix multiplication :

(10) Inverse of matrix :

(11) Matrix multiplication :
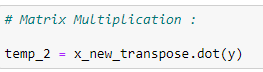
(12) Find the coefficients :
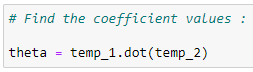
(13) Plot the regression line :
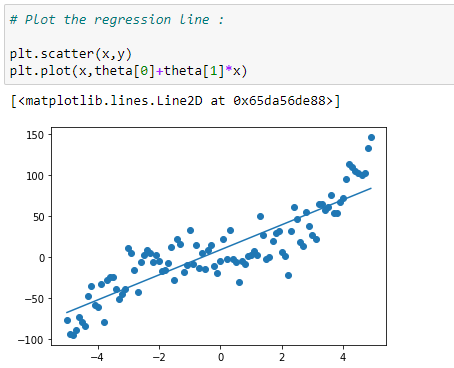
(14) Prediction function :
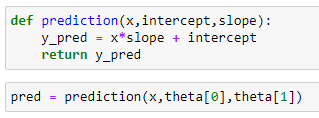
(15) Calculate the mean squared error :
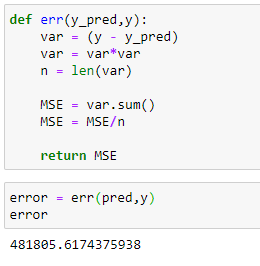
So here we can see that the error is high. Let’s check what happens if we use polynomial equation.
Normal Equation is as follow :
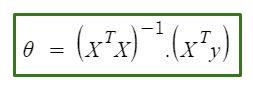
Polynomial Regression :
Hypothesis Function For Polynomial Regression :
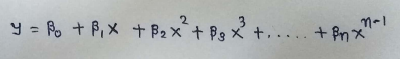
Where,
beta_0 , beta_1, …. are the coefficients that we need to find.
x,x²,x³ are features of our dataset.
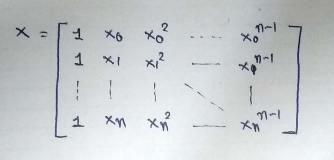
Let’s code :
(1) Import required libraries :
(2) Generate data points :
(3) Initialize x,x²,x³ vectors :
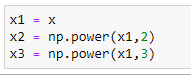
(4) Column-1 of X matrix :
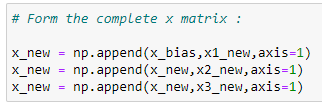
(5) Form the complete x matrix :
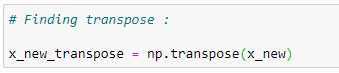
(6) Transpose of matrix :
(7) Matrix multiplication :

(8) Inverse of a matrix :
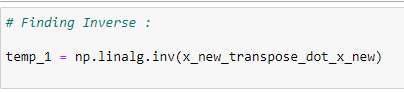
(9) Matrix multiplication :
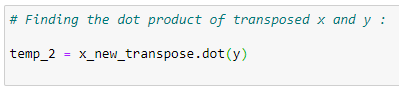
(10) Coefficient values :
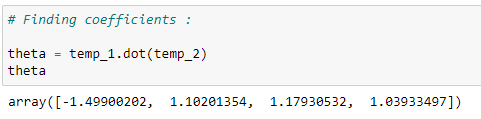
(11) Store the coefficients in variables :
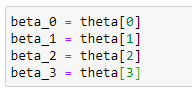
(12) Plot the data with curve :
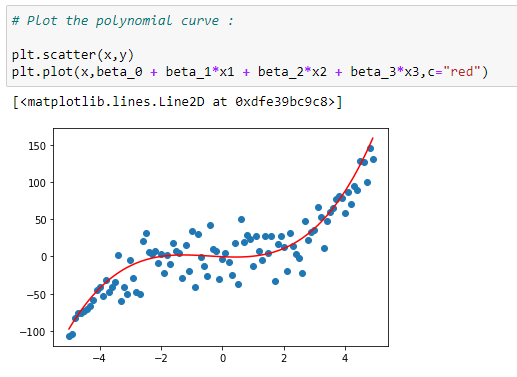
(13) Prediction function :
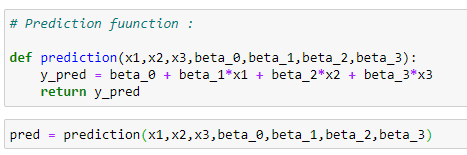
(14) Error function :

(15) Calculate the error :
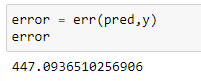
Here you can see that the error is significantly lower than the error in linear regression.
So we can say that it has done a pretty good work. So in conclusion we can say that if our dataset if following curve trends then we can use polynomial regression for better results and accuracy.
I hope you guys enjoyed this article. Please hit the clap icon if you liked it.
Moving Forward,
In the next article I will show how we can implement other polynomial regressions in python.
All my articles are available on my blog :
patrickstar0110.blogspot.com
Watch detailed videos with explanations and derivation on my youtube channel :
https://www.youtube.com/channel/UCpRJj1vjQsjCTB3S5ANvNvg
(1) Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch :
https://youtu.be/bM3KmaghclY
(3) Simple Linear Regression Using Sklearn :
https://youtu.be/_VGjHF1X9oU
(4) Machine Learning Mathematic (Matrices) Explained :
https://youtu.be/1MASyeyAydw
(5) Complete Mathematical Derivation Of Normal Equation:
https://youtu.be/E7Q4UP6bNmc
(6) Simple Linear Regression Implementation Using Normal Equation:
https://youtu.be/wmmUJnmwQho
Read my other articles :
(1) Linear Regression From Scratch :
https://medium.com/@shuklapratik22/linear-regression-from-scratch-a3d21eff4e7c
(2) Linear Regression Through Brute Force :
https://medium.com/@shuklapratik22/linear-regression-line-through-brute-force-1bb6d8514712
(3) Linear Regression Complete Derivation:
https://medium.com/@shuklapratik22/linear-regression-complete-derivation-406f2859a09a
(4) Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
(5) Simple Linear Regression From Scratch :
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-2fa88cd03e67
(6) Gradient Descent With it’s Mathematics :
https://medium.com/@shuklapratik22/what-is-gradient-descent-7eb078fd4cdd
(7) Linear Regression With Gradient Descent From Scratch :
https://medium.com/@shuklapratik22/linear-regression-with-gradient-descent-from-scratch-d03dfa90d04c
(8) Error Calculation Techniques For Linear Regression :
https://medium.com/@shuklapratik22/error-calculation-techniques-for-linear-regression-ae436b682f90
(9) Introduction to Matrices For Machine Learning :
https://medium.com/@shuklapratik22/introduction-to-matrices-for-machine-learning-8aa0ce456975
(10) Understanding Mathematics Behind Normal Equation In Linear Regression (Complete Derivation)
https://medium.com/@shuklapratik22/understanding-mathematics-behind-normal-equation-in-linear-regression-aa20dc5a0961
(11)Implementation Of Simple Linear Regression Using Normal Equation(Matrices)
https://medium.com/@shuklapratik22/implementation-of-simple-linear-regression-using-normal-equation-matrices-f9021c3590da
(12) Multivariable Linear Regression Implementation :
https://medium.com/@shuklapratik22/multivariable-linear-regression-using-normal-equation-707d19f1c325

No comments:
Post a Comment