
What is least square property?
Form the distance (y — y’) between each data point (x,y) and a potential regression line y’ = mx +b. Each of these differences is known as a residual. Square these residual and sum them. The resulting sum is called residual sum of squares or SSres. The line that “best fits” has the least possible value of SSres.
In the last article we saw how to find the equation of line when two points are given. But what if we have more than 2 points? In this article we’ll see how to find the regression that “best fits” our data( i.e. minimum error). In this article we’ll see about the brute force attack to find the regression line.
We’ll find the regression line for the following data:
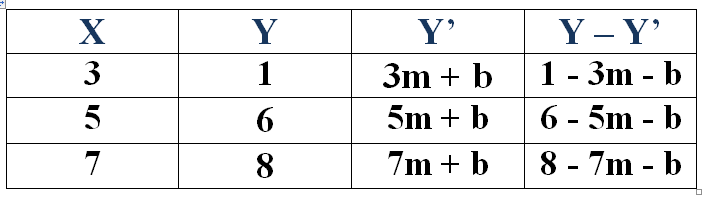
Now we have to find the square of each row in Y — Y’.
As we all know :
![]()
Finding the values :
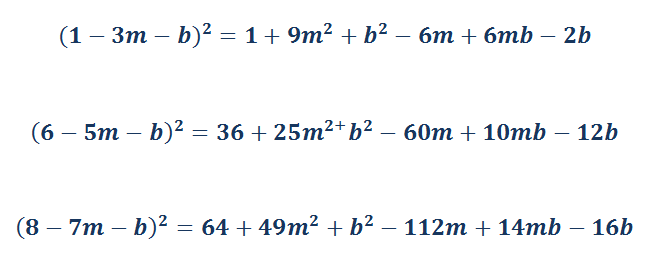
After adding all the values we get :
![]()
Now, remember the vertex of ax²+bx+c :
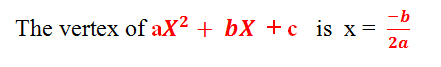
For example : The vertex of 2x²+3x+6 will be…… : (-3/4)
So, here in our equation we can easily find two equations for with variables m and b in it. Here’s how to find it.
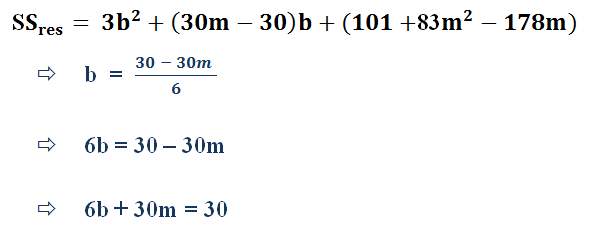
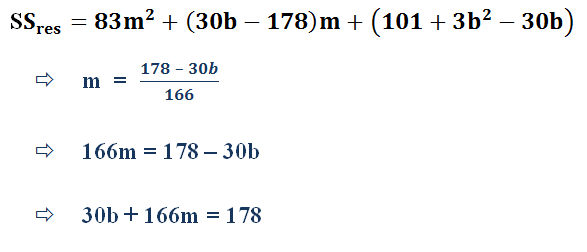
Now solving the two equations we get …..
m = 7/4 = 1.75
b = -15/4 = -3.75
So, in the end our equation Y = mX + b will be ……….
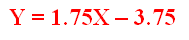
Here’s how our regression line looks on coordinate plane :
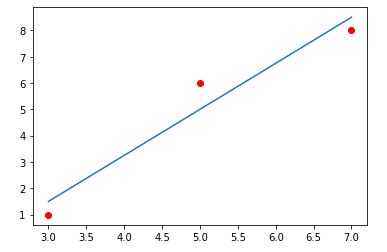
To conclude, in this article we saw how we can find the line that “best fits” the given data points. But as you can see this is very time consuming approach. We generally use python libraries to perform such tasks. But we must know the logic behind each algorithm, right? So in the next article we’ll see how we can perform such calculations using a single formula and we’ll also see about how that formula is derived.
*******
Moving forward,
In the next article we’ll see about the derivation of simple linear regression formula.
You can download the code and some handwritten notes on the derivation from here : https://drive.google.com/open?id=1_stSoY4JaKjiSZqDdVyW8VupATdcVr67
If you have any additional questions, feel free to contact me : shuklapratik22@gmail.com
No comments:
Post a Comment