
Normal Equation is an analytic approach to Linear Regression with a least square cost function. We can directly find out the value of θ without using Gradient Descent. Following this approach is an effective and time-saving option when we are working with dataset with small features.
Normal Equation is as follows :
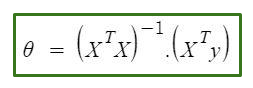
In the above equation :
θ : hypothesis parameters that define it the best.
X : input feature value of each instance
Y :Output value of each instance
Derivation Of Normal Equation:
(1) Hypothesis function :
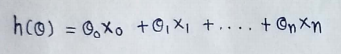
Where,
n : number of features in the dataset.
X0 = 1 (for vector multiplication)
(2) Vector θ :
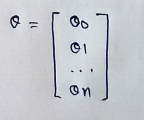
(3) Vector X:
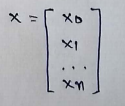
(4) Notice that there is a dot product between θ and X. So we can write this as :
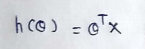
(5) Cost function :
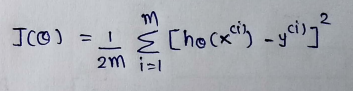
Xi = the input value of ith trining example.
m : number of training instances.
n : number of dataset features
yi = the expected result for i th instance
(6) Representing the cost function in vector form:
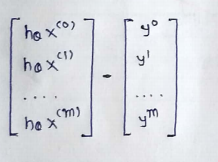
(7) We are going to ignore 1/2m here since it’s not going to make any difference in the derivation.
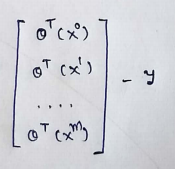
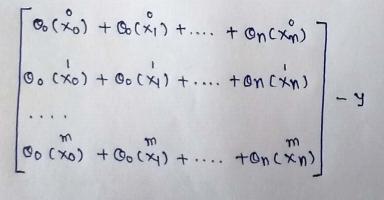

(8) This can further be reduced to :
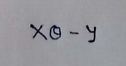
(9) But in our cost function there is a square. We can’t simply square the above expression. As the square of vector/matrix is not equal to square of it of its values. so to get the squared values,multiply the vector/matrix with it’s transpose.
In this article I’m going to show some basic operations that we can perform on matrices like addition, multiplication…medium.com
Find equation is :
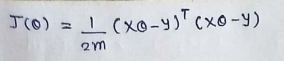
(10) Ignore the 1/2m since it’s not going to make any difference in out derivation.
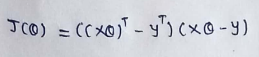
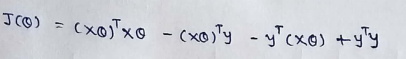
(11)Now in the above equation 2nd and 3rd terms are same.(Explained in my previous article.) So add them.
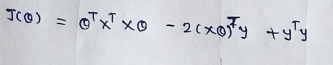
(12) Our ultimate goal is to minimize the cost function.Finding derivatives.
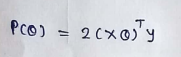
(13) Writing it in a vector form :
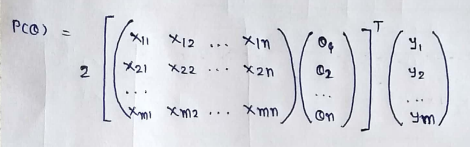
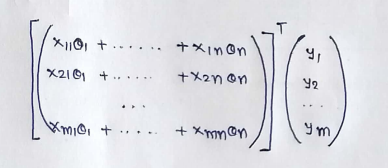
(14) Multiplying the vectors:
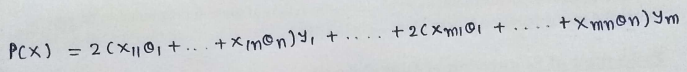
(15) Simplifying it a bit :

(16) Find the derivatives :
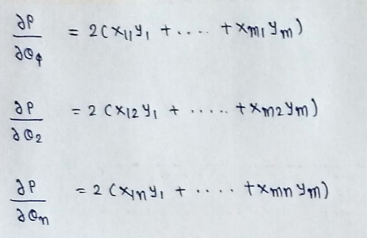
(17) In Conclusion:
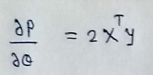
(18) Finding the other derivative:
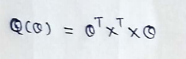
(19)Writing in vector form :
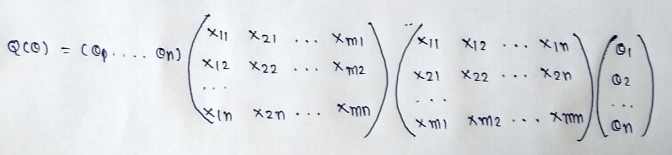
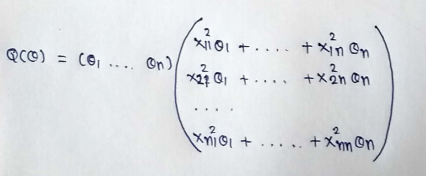
(20) Simplifying :
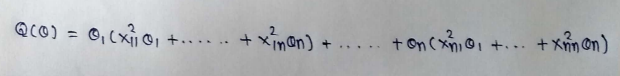
(21) Finding partial derivative :
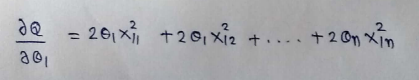
(22) Finding derivative of last remaining term. It will be 0, as there is no theta in that.
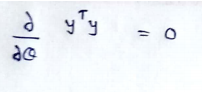
(23) Combining all together :
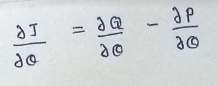
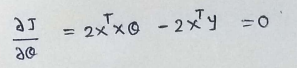
(24) Simplifying :
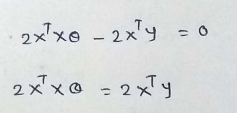
(25) Final step :
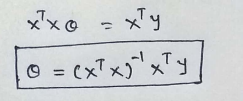
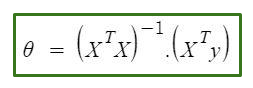
That’s it. We’ve derived our Normal Equation from scratch. I hope you guys enjoyed it!
Moving Forward,
In the next article I will show you how we can implement Linear Regression using the Normal Equation we just derived.
For more such detailed descriptions on machine learning algorithms and it’s derivation and implementation, you can follow me on my blog:
All my articles are available on my blog :
patrickstar0110.blogspot.com
Watch detailed videos with explanations and derivation on my youtube channel :
(1) Simple Linear Regression Explained With It’s Derivation:
https://youtu.be/1M2-Fq6wl4M
(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch :
https://youtu.be/bM3KmaghclY
(3) Simple Linear Regression Using Sklearn :
https://youtu.be/_VGjHF1X9oU
Read my other articles :
(1) Linear Regression From Scratch :
https://medium.com/@shuklapratik22/linear-regression-from-scratch-a3d21eff4e7c
(2) Linear Regression Through Brute Force :
https://medium.com/@shuklapratik22/linear-regression-line-through-brute-force-1bb6d8514712
(3) Linear Regression Complete Derivation:
https://medium.com/@shuklapratik22/linear-regression-complete-derivation-406f2859a09a
(4) Simple Linear Regression Implementation From Scratch:
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-from-scratch-cb4a478c42bc
(5) Simple Linear Regression From Scratch :
https://medium.com/@shuklapratik22/simple-linear-regression-implementation-2fa88cd03e67
(6) Gradient Descent With it’s Mathematics :
https://medium.com/@shuklapratik22/what-is-gradient-descent-7eb078fd4cdd
(7) Linear Regression With Gradient Descent From Scratch :
https://medium.com/@shuklapratik22/linear-regression-with-gradient-descent-from-scratch-d03dfa90d04c
(8) Error Calculation Techniques For Linear Regression :
https://medium.com/@shuklapratik22/error-calculation-techniques-for-linear-regression-ae436b682f90
(9) Introduction to Matrices For Machine Learning :
https://medium.com/@shuklapratik22/introduction-to-matrices-for-machine-learning-8aa0ce456975

No comments:
Post a Comment