Linear Regression With Gradient Descent From Scratch

In the last article we saw that how the formula for finding the regression line with gradient descent works. In that article we started with some basic cost function and then made our way through our original cost function which was Mean Squared Error(MSE). I recommend you to read that article first,if you haven’t already!

All my articles are available on my blog : patrickstar0110.blogspot.com

Here we will use a slightly different cost function that MSE. Here we will use our basic Sum of Squared Residual (SSR) function to find the optimal parameter values. First we’ll find the parameters for one iteration by hand. That will give us ample idea of how this algorithm works.

So what are we waiting for? Let’s dig in!

Gradient Descent For Linear Regression By Hand:

In this, I will take some random numbers to solve the problem. But it is also applicable for any datasets. Here we’ll use the SSR cost function for ease of calculations.

(1) Dataset :

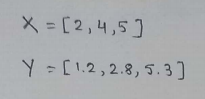
(2) Initial parameter values:

(3) Cost function :

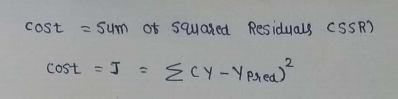
(4) Prediction function :

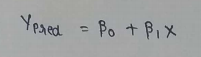
(5) Predicted values :

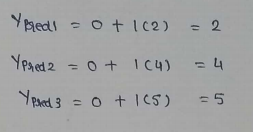
(6) Calculating cost :

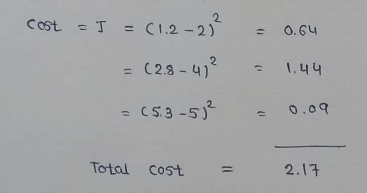
(7) Finding derivatives :

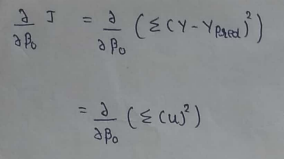
(8) Defining u :

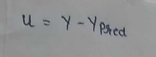
(9) Calculating the derivative :

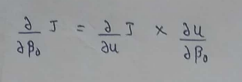
(10) Simplifying :

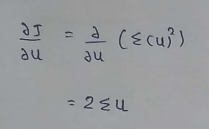
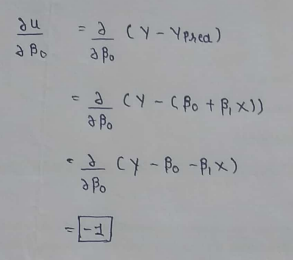
(11) Merging calculated values :

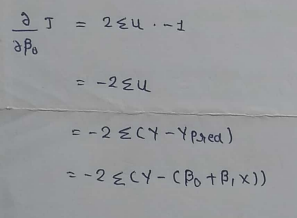
(12) Find the other parameter:

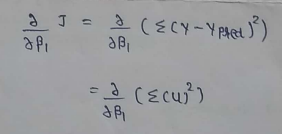
(13) Simplifying:

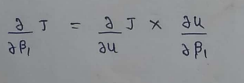
(14) Calculating :

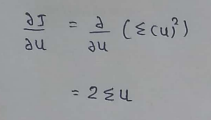
(15) Merging calculated values :

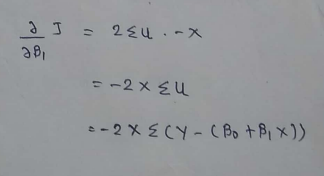
(16) Calculating values for derivatives:

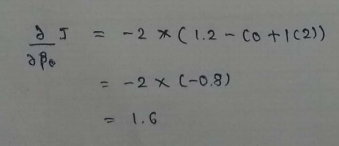
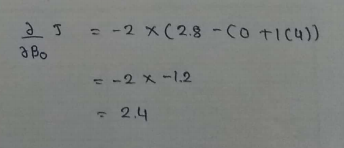
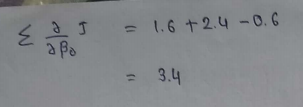
(17) Calculating value for other parameter :

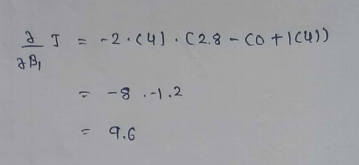
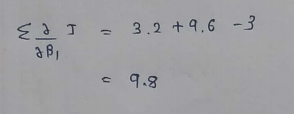
(18) Calculating the step size :

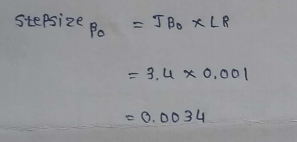
(19) Updating the values :

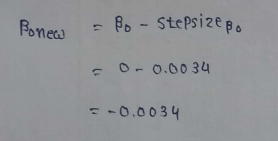
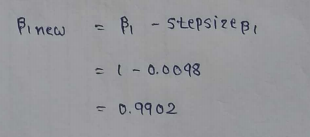
(20) Repeat the same process for all the iterations

*******

Here we can see that if we are going to do 1000 iterations by hand, it is going to take forever for some slow kids like me. That’s why we implement it in python! We will use the derived formulas and some “for” loops to write our python code.

Let’s get started!

Outline of the process :

(1) Initialize beta 0 and beta 1 values.

(2) Initialize learning rate and desired number of iterations.

(3) Make a for loop which will run n times, where n is number of iterations.

(4) Initialize the variables which will hold the error for a particular iteration.

(5) Make prediction using the line equation.

(6) Calculate the error and append it to the error array.

(7) Calculate partial derivatives for both coefficients.

(8) Increase the cost of both coefficients (As there are 3 data points in our dataset.)

(9) Update the values of coefficients.

# Let’s code :

(1) Import some required libraries :

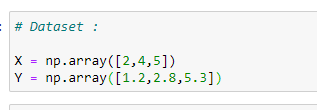
(2) Define the dataset :

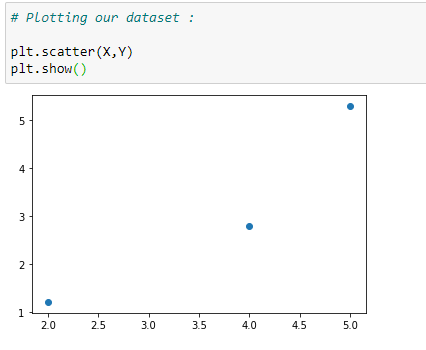
(3) Plot the data points :

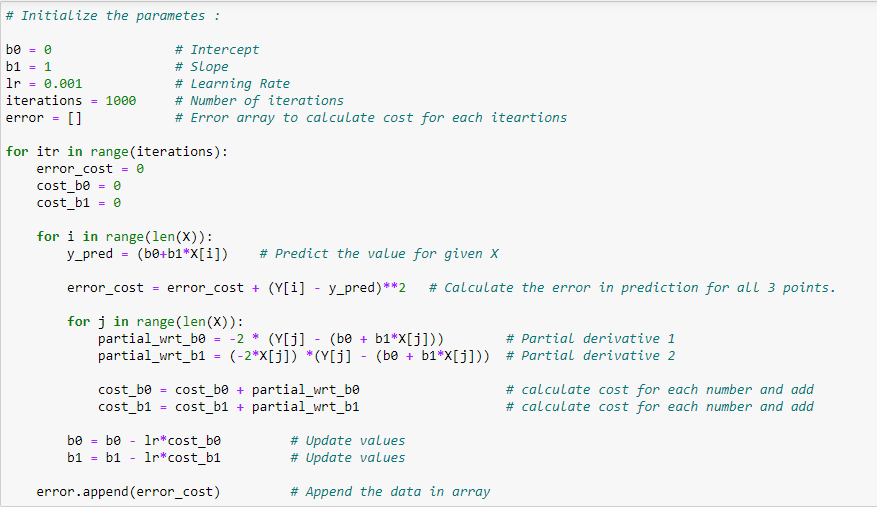
(4) Main function to calculate values of coefficients :

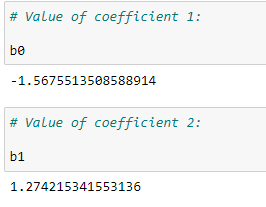
(5) Value of coefficients :

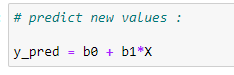
(6) Predicting the values :

(7) Plot the regression line :

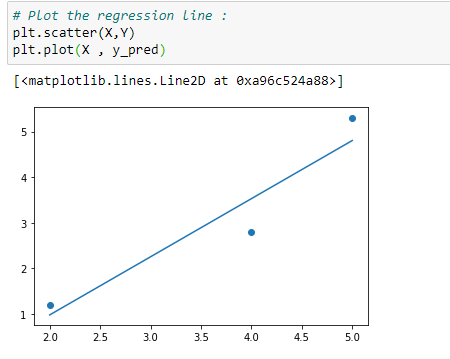
(8) Predicting values :

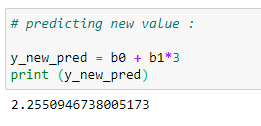
(9) Plotting the error for each iterations :

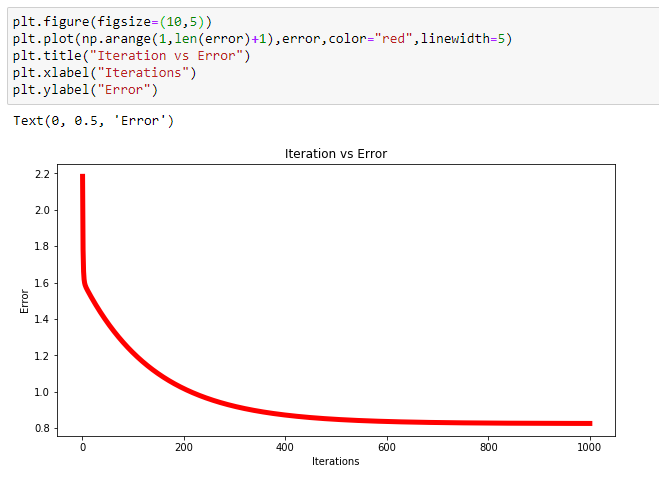
That’s it. We did it! We have our optimal parameters for 1000 iterations and decreased error. However we can see that this method is less efficient if we take into account only a few iterations(i.e. 10).

*******

To find more such detailed explanation, visit my blog: patrickstar0110.blogspot.com

If you have any additional questions, feel free to contact me : shuklapratik22@gmail.com